এবারে আমরা সত্যিকারের বর্তনী বা সার্কিটে সত্যিকারের বিদ্যুৎ প্রবাহ নিয়ে আলোচনা করব। আমরা অনেকবার বলেছি যে দুটি বিন্দুতে যদি পটেনশিয়াল বা বিভব পার্থক্য থাকে এবং আমরা যদি একটি পরিবাহী তার দিয়ে সেই দুটি বিন্দুকে জুড়ে দিই তাহলে বিন্দু দুটির ভেতরে বিদ্যুৎ প্রবাহ হবে, কিন্তু কতটুকু বিদ্যুৎ প্রবাহ হবে সেটি নিয়ে এখনো কিছু বলা হয়নি। শুধু তাই নয় একটা সোনার পরিবাহী তার দিয়ে জুড়ে দিলে যেটুকু বিদ্যুৎ প্রবাহিত হবে একটা লোহার তার জুড়ে দিলেও কি সমান পরিমাণ বিদ্যুৎ প্রবাহিত হবে?
পটেনশিয়াল বা বিভব পার্থক্য এবং তড়িৎ প্রবাহের মাঝে সম্পর্ক দেখার জন্য আমরা একটা এক্সপেরিমেন্ট করতে পারি। বিভব মাপার জন্য যে বক্সটি ব্যবহার করা হয় তার নাম ভোল্টমিটার, বিদ্যুৎ প্রবাহ বা কারেন্ট মাপার জন্য যে যন্ত্র ব্যবহার করা হয় সেটার নাম অ্যামিটার। (আসলে একই যন্ত্রের সুইচ ঘুরিয়ে এটাকে কখনো ভোল্টমিটার বা কখনো অ্যামিটার হিসেবে ব্যবহার করা যায়) আমরা কয়েকটা ব্যাটারি সেল নিতে পারি, একটা ব্যাটারি সেলের জন্য বিভব 1.5 v হলে দুটি ব্যাটারি সেলের জন্য 2 x 1.5= 3 V, তিনটির জন্য 3 x 1.5 = 4.5v এভাবে ভিন্ন ভিন্ন বিভব পার্থক্য প্রয়োগ করতে পারি। শুধু তাই নয়, আমরা ব্যাটারিগুলো উল্টে দিয়ে বিভব পার্থক্যের দিকও পরিবর্তন করে দিতে পারি। কাজেই আমরা যদি একটা তার বা অন্য কোনো পরিবাহীর দুই পাশে একটা বিভিন্ন পজিটিভ এবং নেগেটিভ বিভব পার্থক্য প্রয়োগ করে কতখানি বিদ্যুৎ প্রবাহিত হয়েছে সেটা মাপার চেষ্টা করি তাহলে দেখব
(a) যত বেশি বিভব পার্থক্য তত বেশি বিদ্যুৎ প্রবাহ
(b) বিভব পার্থক্য নেগেটিভ হলে বিদ্যুৎ প্রবাহও দিক পরিবর্তন করছে।
অর্থাৎ
আমরা যদি অন্য কোনো উপাদানের তৈরি একটা তার দিয়ে একই পরীক্ষাটি করি তাহলে একই ধরনের ফলাফল পাব। তবে সরলরেখার ঢালটা হয়তো অন্য রকম হবে। এখন এই দুটি পরীক্ষার ফলাফল যদি বিশ্লেষণ করি তাহলে বুঝতে পারব প্রথমে একটা নির্দিষ্ট বিভব পার্থক্যে যতটুকু বিদ্যুৎ প্রবাহিত হয়েছে দ্বিতীয় বস্তুর জন্য সেই একই বিভব পার্থক্যে বিদ্যুৎ প্রবাহ হচ্ছে কম। প্রথমটিতে যেন বিদ্যুৎ প্রবাহ তুলনামূলকভাবে সহজ, দ্বিতীয়টিতে যেন বিদ্যুৎ প্রবাহের বাধা একটু বেশি। বিষয়টা ব্যাখ্যা করার জন্য বিদ্যুৎ প্রবাহের বাধা (Resistance) বা সত্যি সত্যি রোধ নামের একটা রাশি তৈরি করা হয়েছে। আমরা দেখতে পারি বিভব পার্থক্য এবং বিদ্যুৎ প্রবাহের সম্পর্কটি একটা সূত্র হিসেবে লেখা যায় যেটি ও'মের সূত্র (Ohm's Law) হিসেবে পরিচিত।
অর্থাৎ রোধ বেশি হলে বিদ্যুৎ প্রবাহ হবে কম। রোধ কম হলে বিদ্যুৎ প্রবাহ হবে বেশি।
এই রোধ বা Resistance এর একক হচ্ছে Ohm । এটাকে গ্রিক অক্ষর (সিগমা) দিয়ে প্রকাশ করা হয়। কোনো বৈদ্যুতিক সার্কিটে 1 v বিভব পার্থক্য দেওয়ার পর যদি দেখা যায় 1 A বিদ্যুৎ প্রবাহিত হচ্ছে তাহলে বুঝতে হবে সেই সার্কিটের রোধ 1।
রোধ হচ্ছে বিদ্যুৎ প্রবাহের বাধা, তাই কোনো পদার্থের দৈর্ঘ্য (L) যত বেশি হবে তার বাধা তত বেশি হবে অর্থাৎ রোধও বেশি হবে।
আবার সরু একটা পথ দিয়ে যত সহজে বিদ্যুৎ প্রবাহিত হতে পারবে, চওড়া একটা পথ দিয়ে তার থেকে অনেক সহজে বিদ্যুৎ প্রবাহিত হতে পারবে অর্থাৎ প্রস্থচ্ছেদ (A) যত বেশি হবে রোধ তত কম হবে।
এই দুটি বিষয়কে আমরা যদি একসাথে আনুপাতিক না লিখে সমীকরণ হিসেবে লিখতে চাই তাহলে একটা ধ্রুবক p ব্যবহার করতে হবে। অর্থাৎ রোধ R হচ্ছে
যেখানে ধ্রুবক হচ্ছে
একটা নির্দিষ্ট পদার্থের জন্য হচ্ছে আপেক্ষিক রোধ এবং তাই এর একক হচ্ছে .
| পদার্থ | আপেক্ষিক রোধ ( ) |
| রূপা | |
| তামা | |
| সোনা | |
| গ্রাফাইট | |
| হীরা | |
| বাতাস |
কোনো পদার্থ কতটুকু বিদ্যুৎ পরিবাহী সেটা বোঝানোর জন্য পরিবাহকত্ব বলে একটা রাশি তৈরি করা হয়েছে, যে পদার্থ যত বেশি বিদ্যুৎ পরিবাহী তার পরিবাহকত্ব তত বেশি, যেটা আপেক্ষিক রোধ ( টেবিল 11.01 ) এর ঠিক বিপরীত।
পরিবাহকত্ব এর একক হচ্ছে
এখানে একটা বিষয় মনে রাখতে হবে কোনো পদার্থের রোধ হচ্ছে ইলেকট্রন প্রবাহের বাধা, অণু- পরমাণুগুলো যত বেশি কাঁপাকাঁপি করে একটা ইলেকট্রন তাদের ভেতর দিয়ে যেতে তত বেশি বাধাগ্রস্ত হয়, কিংবা তার রোধ তত বেশি। ভাপমাত্রা বাড়িয়ে দিলে যেহেতু অণু-পরমাণুগুলো বেশি কাঁপাকাঁপি করে ভাই সব সময়ই তাপমাত্রা বাড়ালে পরিবাহী পদার্থের আপেক্ষিক রোধ বেড়ে যায়। সেজন্য যখন কোনো পদার্থের রোধ বা আপেক্ষিক রোধ প্রকাশ করতে হয় তখন তার জন্য তাপমাত্রাটা নির্দিষ্ট করে বলে দিতে হয়।
স্থির মানের রোধ: বিভিন্ন বর্তনী বা সার্কিটে ব্যবহার করার জন্য নির্দিষ্ট মানের রোধ বা রেজিস্টর ব্যবহার করা হয়। এগুলো নানা আকারের এবং নানা ধরনের হতে পারে। ল্যাবরেটরিতে ব্যবহার করার জন্য যে রোধ ব্যবহার করা হয় সাধারণত তার উপরে বিভিন্ন রঙের ব্যান্ডের মাধ্যমে তার মান প্রকাশ করা হয়। একটি রোধের মান ছাড়াও সেটি কত বৈদ্যুতিক ক্ষমতা সহ্য করতে পারবে সেটিও নির্দিষ্ট করে দেওয়া থাকে।
পরিবর্তী রোধ: মাঝে মাঝেই কোনো ইলেকট্রিক সার্কিটে একটি রোধের প্রয়োজন হয়, যেটির মান প্রয়োজনমতো পরিবর্তন করা যেতে পারে। যে ধরনের রোধের মান একটি নির্দিষ্ট সীমার ভেতরে পরিবর্তন করা যায় সেটিকে পরিবর্তী রোধ বা রিওস্টেট বলে। স্থির রোধের দুটি প্রাঙ্ক থাকে, পরিবর্তী রোখে দুই প্রান্ত ছাড়াও মাঝখানে আরেকটি প্রান্ত থাকে, যেখানে পরিবর্তন করা রোধের মানটুকু পাওয়া যায়।
পরিবাহীতে তাপমাত্রা বাড়ালে রোধ বেড়ে যায় কিন্তু সেমিকন্ডাক্টরের বেলায় ঠিক তার উল্টো ব্যাপারটা ঘটে। সেমিকন্ডাক্টরে তাপমাত্রা বাড়ালে রোধ কমে যায়। তার কারণ কন্ডাক্টরে যেমন বিদ্যুৎ প্রবাহের জন্য মুক্ত ইলেকট্রন রয়েছে সেমিকন্ডাক্টরে তা নেই। সেখানে তাপমাত্রা বাড়ালেই শুধু কিছু ইলেকট্রন বিদ্যুৎ প্রবাহের জন্য পাওয়া যায়। তাই সেখানে তাপমাত্রা বাড়ালে রোধ কমে যায়।
আমরা যদি ও'মের সূত্র বুঝে থাকি তাহলে আমরা এখন সার্কিট বিশ্লেষণ করতে পারি। সেটা করার আগে সার্কিটে ব্যবহার করা হয় এ রকম কয়েকটি প্রতীকের সাথে আগে পরিচিত হয়ে নিই: (চিত্র 11.07)
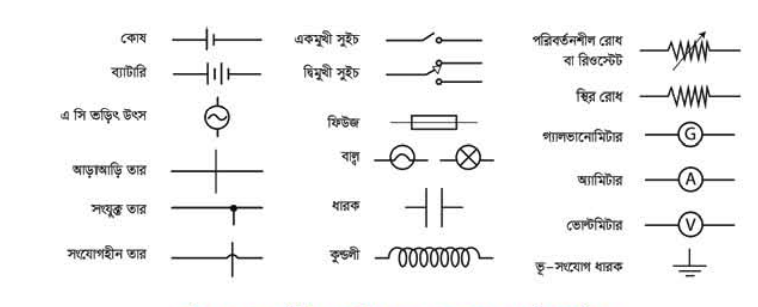
চিত্র 11.7; সার্কিট বা বর্তনীতে ব্যবহার করা হয় এ রকম কিছু প্রতীক
সব পদার্থেরই কিছু না কিছু রোধ আছে কিন্তু আমাদের দৈনন্দিন জীবনে সার্কিটে ব্যবহারের সময় বৈদ্যুতিক তারের রোধকে আমরা ধর্তব্যের মাঝে নিই না। যখন রোধ প্রয়োজন হয় তখন আমরা বিশেষভাবে তৈরি বিভিন্ন মানের রোধ ব্যবহার করি। কখনো কখনো বিশেষ প্রয়োজনে এমন রোধ ব্যবহার করা হয় যেখানে তার মানটি পরিবর্তনও করা যায়, এগুলোকে পরিবর্তনশীল রোধ বলে।
কোনো সার্কিট বিশ্লেষণ করতে হলে নিচের কয়েকটা সোজা বিষয় মনে রাখাই যথেষ্ট;
(a) বিদ্যুতের উৎসের (ব্যাটারি সেল, জেনারেটর যাই হোক) উঁচু পটেনশিয়াল থেকে যে পরিমাণ বিদ্যুৎ বের হয় পুরো সার্কিটের ভেতর দিয়ে প্রবাহিত হয়ে ঠিক সেই পরিমাণ বিদ্যুৎ কম পটেনশিয়ালে ফিরে আসে।
(b) সার্কিটের যেকোনো জায়গার যেকোনো বিন্দুতে যে পরিমাণ বিদ্যুৎ ঢোকে ঠিক সেই পরিমাণ বিদ্যুৎ বের হয়ে যায়, সার্কিটের ভেতরে বিদ্যুতের কোনো সৃষ্টি বা ধ্বংস নেই।
(c) সার্কিটের ভেতরে যেকোনো অংশের দুই বিন্দুতে ওহমের সূত্র সব সময় সত্যি হবে, অর্থাৎ সেই দুই অংশের যে পরিমাণ বিভব পার্থক্য রয়েছে ডাকে সেই অংশের রোধ দিয়ে ভাগ দিলেই তার ভেতর দিয়ে প্রবাহিত বিদ্যুৎ বের হয়ে যাবে।
আমরা এখন যেকোনো বর্তনী বা সার্কিট বিশ্লেষণ করতে প্রস্তুত। একটা সার্কিটের যেকোনো অংশ দিয়ে কতটুকু বিদ্যুৎ প্রবাহিত হচ্ছে এবং যেকোনো অংশের বিভব কত সেটা জানলেই আমরা ধরে নেব সার্কিটটা আমরা পুরোপুরি বুঝে গেছি। একটা সার্কিটে ব্যাটারি সেল, রোধ, ক্যাপাসিটর, ডায়োড, ট্রানজিস্টর অনেক কিছু থাকতে পারে। তবে আমরা আপাতত শুধু ব্যাটারি সেল আর রোধ দিয়ে তৈরি সার্কিট বিশ্লেষণ করব। সার্কিটে বিভিন্ন রোধ তামার তার দিয়ে সংযুক্ত করা হয়, যদিও আমরা দেখেছি তামারও একটি আপেক্ষিক রোধ আছে। কিন্তু বাস্তব জীবনে সার্কিটে যে রোধ ব্যবহার করা হয় তাদের তুলনায় এটি এত কম যে আমরা এটাকে ধর্তব্যের মাঝেই আনব না। ধরে নেব তারের রোধ নেই। কাজেই একটা তারের সব জায়গায় বিভব সমান।
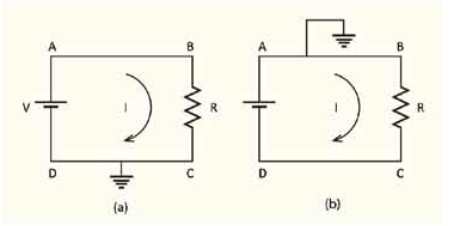
চিত্র 11.08: আক্রি ব্যাটারি সেল এবং একটি রোধ সংযুক্ত দুটি বর্তনী বা সার্কিট
এবারে 11.08a চিত্রে দেখানো একটা বর্তনী বিশ্লেষণ করা যাক, এখানে একটা রোধকে দুটো তার দিয়ে একটা ব্যাটারি সেলের দুই মাথায় লাগানো হয়েছে। যেহেতু CD অংশটুকু ভূমিসংলগ্ন করা হয়েছে তাই আমরা বলতে পারব ব্যাটারি সেলের নিচের প্রান্তটির বিভব হচ্ছে শূন্য। তাই ব্যাটারির উপরের প্রান্তের বিভব V এবং BC অংশে একটা রোধ, রোধের দুই পাশে বিভব পার্থক্য হচ্ছে
কাজেই রোধ যদি R হয় তাহলে এর ভেতর দিয়ে যে বিদ্যুৎ I প্রবাহিত হচ্ছে তার মান
কাজেই ব্যাটারির A থেকে I বিদ্যুৎ বের হয়ে B বিন্দুতে ঢুকে যাচ্ছে। আমরা এই সার্কিটের প্রত্যেকটা বিন্দুতে বিভব আর বিদ্যুৎ বের করে ফেলেছি।
ধরা যাক হুবহু একই সার্কিটে আমরা যদি DC অংশ ভূমিসংলগ্ন না করে AB অংশ ভূমিসংলগ্ন করি (চিত্র 11.02b) তাহলে কী হবে? ব্যাটারি সেলটা যেহেতু V ভোল্টের তাই A এবং D এর পার্থক্য v থাকতেই হবে, যেহেতু A এর বিভব শূন্য তাই D এর বিভব নিশ্চয়ই -V. কাজেই B এবং C এর বিভব পার্থক্য
ভেতরকার রোধ R, কাজেই বিদ্যুৎ প্রবাহ:
অর্থাৎ ঠিক আগের মান, যেটাই হওয়ার কথা। লক্ষ করো পটেনশিয়ালের মান পরিবর্তন হয়েছে কিন্তু পার্থক্য পরিবর্তন হয়নি।
এবারে কোনো বর্তনীতে একাধিক রোধ থাকলে সেগুলোকে কীভাবে একটি ভুল্য রোধ হিসেবে বিবেচনা করা যায় আমরা সেই বিষয়টি দেখে নেই । 11.03 চিত্রের সার্কিটে দুটো রোধ লাগানো আছে, যেহেতু C ভূমিসংলগ্ন তাই তার বিভব শূন্য এবং A এর বিভব V। আমরা B এর বিভব কত জানি না, কিন্তু এটুকু জানি যে এবং দুটোর ভেতর দিয়েই সমান পরিমাণ বিদ্যুৎ I প্রবাহিত হচ্ছে। আমরা এমনিতেই বলে দিতে পারি যে দুটো রোধের যোগফলটি হবে মোট রোধ R এবং বিদ্যুৎ প্রবাহ হবে 1 = V/R কিন্তু সেভাবে না লিখে আমরা বরং এটা প্রমাণ করে ফেলি।
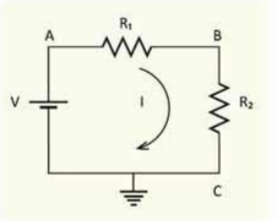
চিত্র 11.11: একটি বর্তনী বা সার্কিটে দুটি রোধ পরপর লাগানো।
যদি ধরে নিই B এর বিভব তাহলে প্রথম রোধএর জন্য লিখতে পারি:
আবার দ্বিতীয় রোধ এর জন্য লিখতে পারি :
কাজেই
কাজেই
আমরা এবং এই দুটি রোধকে একটি রোধ হিসেবে কল্পনা করতে পারিঃ
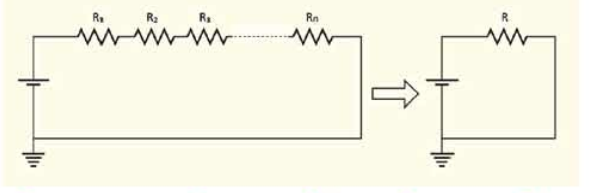
চিত্র 11.12: অনেক গুলো পর্যায়ক্রম রোধকে একটি তুল্য রোধ হিসেবে কল্পনা করা যায়।
যদি এখানে দুটি না হয়ে তিন-চারটি বা আরো বেশি রোধ থাকত (চিত্র 11.12) তাহলেও আমরা দেখাতে পারতাম যে সেগুলোকে সম্মিলিতভাবে একটি রোধ R কল্পনা করতে পারি বেটি সবগুলো রোধের যোগফলের সমান। এটাকে তুল্য রোধ বলে। অর্থাৎ যখন কোনো সার্কিটে রকম অনেকগুলো রোধ পরপর থাকে (শ্রেণি বর্তনী} তখন তাদের তুল্য রোধ
এবারে আমরা রোধগুলো পরপর না রেখে সমান্তরালভাবে রাখব (চিত্র 11.13)। এই সার্কিটে আমরা বিভিন্ন বিন্দুকে A, B, C, D, E এবং F নাম দিয়েছি। চিত্রটি দেখেই বোঝা যাচ্ছে D, E এবং F বিন্দু ভূমিসংলগ্ন হওয়ার এই বিন্দুগুলোর বিভব শূন্য। কাজেই A, B এবং C বিন্দুতে বিভব V. ব্যাটারি সেল থেকে । কারেন্ট বের হয়েছে।
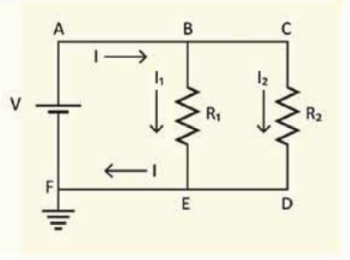
চিত্র 11.13: একটি সার্কিটে দুটি রোধ সমান্তরাল্ভাবে রাখা
এই বিদ্যুৎ B বিন্দুতে দুই ভাগে ভাগ হয়ে এবংরোধের ভেতর দিয়ে যথাক্রমে এবং হিসেবে প্রবাহিত হয়ে E বিন্দুতে একত্র হয়ে হিসেবে ব্যাটারি সেলে ফিরে যাচ্ছে। আমরা আগেই বলেছি সার্কিটে ব্যাটারি থেকে বিদ্যুৎ বের হয়, সার্কিটে ঘুরে আবার ব্যাটারি সেলে ফিরে যায়। পুরো সার্কিটে এর বাইরে কোনো বিদ্যুতের জন্ম হতে পারে না, আবার ক্ষয়ও হতে পারে না। তাই
এখন আমরা এবং কত হবে বের করতে পারি
কাজেই
অর্থাৎ এবারেও আমরা একটা তুল্য রোধ R সংজ্ঞায়িত করতে পারি যেখানে
এবং
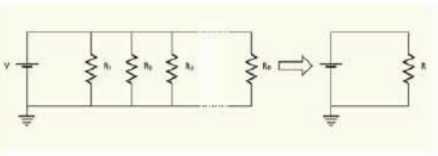
চিত্র 11.14: অনেকগুলো সমান্তরাল রোধ বা রেজিস্ট্ররকে একটি তুল্য রোধ বা রেজিস্ট্রর হিসেবে কল্পনা করা যায়।
এখানে যদি দুটো না হয়ে আরো বেশি রোধ থাকে (চিত্র 11.14) তাহলেও আমরা দেখতে পারি: তুল্য রোধ R হচ্ছে
Read more